Problem Link:

Contest
Practice

Author:Parth Trehan
Editorialist:Parth Trehan

Difficulty:

Easy-Medium

Prerequisites:

Graph Theory, BFS

Problem:

We need to traverse a graph from node 1 to node N. Some nodes of the graph are dependent on other nodes i.e. we can cross/pass some nodes iff we have already visited the nodes provided in the information.

Explanation:

We maintain our graph in an adjacency list. We even maintain an array with the extra information. Now, we traverse this graph from node 1 using the BFS graph traversal technique. As usual we maintain a queue for the BFS traversal. In addition to the given contraint, we maintain another queue. If we are able to pass a node i.e. no extra information is entered about it, we simply mark the node visited. If we come across a node whose entry is present in the extra information, if we have already visited the node associated to it, we simply treat it as a regular node and mark it as visited too but the node associated to it is node visited, we push it in our other queue and remove it's entry from the queue we maintained for BFS traversal. After we have visited all the possible visitable nodes, we check our newly manitained queue. If some nodes are now visitable, we push those nodes back in our BFS queue and start the traversal again. In the process, if we pass through the Nth node, we return back to the calling function. Now, if at end, all the visitable nodes are visited and the nodes present in the new maintained queue cannot be visited according to the constraint, it will leave our BFS traversal queue empty and this could be the condition using which we would break out of the loop.

Solution:

Setter's solution

Problem Link:

Contest
Practice

Author:Parth Trehan
Editorialist:Parth Trehan

Difficulty:

Simple

Problem:

Count the number of pairs that can be formed holes in a character and the number of pairs of non-hold characters.

Explanation:

Given are two strings, we need to compare the two strings on a given constraint called the "toingness", which is nothing but the sum of pair of total holes and the pair of character that do not contain any hole. The number of holes in a character is given below: A-1 B-2 C-0 D-1 E-0 F-0 G-0 H-0 I-0 J-0 K-0 L-0 M-0 N-0 O-1 P-1 Q-1 R-1 S-0 T-0 U-0 V-0 W-0 X-0 Y-0 Z-0 1-0 2-0 3-0 4-1 5-0 6-1 7-0 8-2 9-1 0-1 a-1 b-1 c-0 d-1 e-1 f-0 g-1 h-0 i-0 j-0 k-0 l-0 m-0 n-0 o-1 p-1 q-1 r-0 s-0 t-0 u-0 v-0 w-0 x-0 y-0 z-0 To calculate the "toingness", just add the total number of holes and the total number of characters without any hole. The toingness then can be calculated by formula:

$toingness = (total holes)/2 + (total characters without any holes)/2$

Both the strings can be compared on the basis of the given attribute.

Time complexity: O(n) where n is the length of the string with maximum length

Solution:

Setter's solution

Problem Link:

Contest
Practice

Author:Parth Trehan
Editorialist:Parth Trehan

Difficulty:

Easy-Medium

Prerequisites:

DP,Maths

Problem:

Given N number of enitities, we need to find the number of ways those entities could either occur independently or in pair.

Explanation:

We are given N entities as an integer input. We need to calculate the number of ways theses entities could either exist independently or in pair. For this purpose, we maintain an array which stores the number of ways that are possible when the enitities are equal to the indeces of the array. Now, for a single entity, it can either exist in a pair or it can exist independently. If there is just one entity, it always occurs independently and if there are two entities, there are two ways for them to exist. Using these two as the base conditions and the recurrence relation $ dp[i] = (dp[i-1] + (i-1)*dp[i-2]) mod 1000000007 $, we can calculate the number of ways and store them in the array. The required array is stored in dp[n].

Solution:

Setter's solution

Found this question on web

An array consists of number of employees required for each month. ‘Hire’ is the cost of hiring an employee and ‘serv’ is the cost of removing an employee and ‘sal’ is the cost of retaining an employee for a month.Cost for each month will be (no_hires * hire + no_fired * serv + no_retain * sal) Given, the requirement for any month will strictly lie between 1 and 41. What is the minimum possible total cost for the ‘n’ months.

Link:https://stackoverflow.com/questions/47032975/solution-company-hiring

How to start ,i think there are many possibilities here ,How to approach??

i have understood the formula for it but i am unable to understand that when k=-1 and n and m have different parity the answer will be -1 but for k=1 answer will not be -1 why?problem

what will be the ans of ( (10^9 + 9)/6 ) % (10^9 + 7) and ( 2/6 ) % (10^9 + 7)

Please post any updates you get here.

Hello Guys

I have divided problems into posts according to difficulty. Hope u all don't mind this. ;)

This is the part 2 of two posts of unofficial editorials for November Long Challenge.

For editorials of problems VILTRIBE, CLRL, PERPALIN and CHEFHPAL, click here.

This post has editorials for problems SEGPROD and CSUBQ.

Problem SEGPROD

Problem Difficulty : Medium

Prerequisites:Modular Multiplicative Inverse (euclid's method), Simple maths, and patience.

Problem Explanation

Given an array and a number P (not necessarily prime), Answer range product queries modulo P. (Not as simple as it looks).

Solution

The first thing i want you all understood is the euclid method of finding modular multiplicative inverse, vital to my approach, about which you may read from wikipedia and find the algorithm here.

The naive brute force (not at all successful even for 20 points, due to integer overflow) would be to create a prefix product array (similar to prefix sum array) and for every query L to R, output prefixProd(R) / prefixProd(L-1) and output modulo P. That's correct, but incapable of giving us 100 points.

So, we move to modular multiplicative inverse (MMI) for help!!. We will to the same thing. Instead of prefix product, we will make an array storing prefix modular product (mod P ofcourse). Now, to answer queries, we are going to answer queries just as prefixModProduct(R)/prefixModProduct(L-1).

This is same as (prefoxModProduct(R) * ModInverse(L-1))%P.

If you have followed the logic upto here and understood MMI from geeksforgeeks page, you have earned 20 points. Hurray.

The reason of only 20 points is that Modular multiplicative inverse of a number A exists only when A and P are co-prime (gcd(A,P)==1). For first subtask, it was given that P is prime and all numbers are smaller than P. From that, it's obvious that gcd(A, P) is one for every element, so we get 20 points.

Now, for full solution, we will use the same technique, but with a slight change in plan. Now, we will first find prime factors of P (U'll understand why) and handle numbers in a different way, which will be explained by an example.

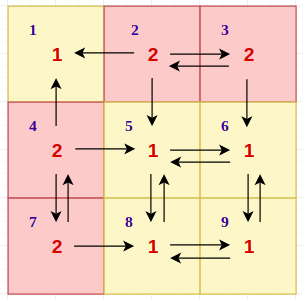
Suppose P = 6 and given array is 1 2 3 4 5 6 7 8 9 10

Now, Prime factors of 6 are 2 and 3.

Now, we will handle powers of 2,3 separately and rest numbers separately.

Create an array factors which will have value {2,3} for this example. create a 2d array factorPowSum[NumberOfFactors][N]

factorPowSum array will look like below (explained how to make this below that)

factor 0 1 2 3 4 5 6 7 8 9 10 11

2..... 0 0 1 1 3 3 4 4 7 7 8 8 (dots to adjust position, spaces are truncated automatically)

3..... 0 0 0 1 1 1 2 2 2 4 4 4

And we will think(it's necessary) we are given given array 1 1 1 1 5 1 7 1 1 5 11 (all numbers are divided by 2 and 3). Now, you will see that all numbers are co-prime to 6. Now we can use the algorithm to solve the queries for reduced array.

Let's assign factor 2 to index 0 and factor 3 to index 1.

Creation of factPowSum array

Just assign factPowSum{factorIndex}{0} = 0 and for 0<i<=N

factPowSum{factorIndex}{i} = factPowSum{factorIndex}{i-1} + Power of factor divided from ith number(1-based indexing).

For example, from 8, 3rd pow of 2 was divided, factorPowSum{0}{3} = factorPowSum{0}{4} + 3.

Hope i made the array clear.

Now, consider that we are given only powers of factors of P.

Continuing same example, The same array we were working with now becomes (I know this is lengthy as hell, but I tried making it as easy to understand as possible)

1 2 3 4 1 6 1 8 9 2 1 (Only powers of 2 and 3 are considered from given array).

Now, if someone ask us range query on this array, we can answer each query within O(number of factors of P) time.

This is simple, just refer to factPowSum array and give it a try. Read further only after a try.

let ans = 1.

for every factor of P, ans = ans*pow(factor, factPowSum{R+1}-factPowSum{L}).

Now, combining above two sub-problems, we get answer of query as

let ans = (prefixModProd(R+1)*MMI(L) * product(pow(factor, factPowSum[R+1]-factPowSum[L])) )%P.

// The queries in question are 0-indexed

You are about to lose 100 points if you do this. Shocked!!. Be sure to take modulo after every multiplication so as to lose your AC to Integer overflow, use long long int/long only.

Now you all deserve 100 points in this problem, but you will get TLE because test cases were too tight. Calculating powers with fast modulo exp even takes O(logN) time, which is too much for 10^7 queries. So we calculate powers of factors of P before answering queries and store in an array. I am not going to explain this but it's easily understandable from my code. In case you need help, feel free to ask.

Added Proof:

lemma: P can have at most 10 different prime factors.

Proof: Try multiplying first eleven prime numbers. The product will be greater than 10^9. but as P <= 10^9, it follows that maximum number of distinct prime factors P can have is 10.

Here's a link to my Code. (Took nearly 30 submissions for 100 points :D)

Problem CSUBQ

Problem difficulty:Medium

Prerequisites:Segment Tree, Too much patience unless u r a segment tree expert (msg me if u are, want a talk.)

Problem Explanation

An array of Size N and M queries, Tow Integers L and R (L<=R), handle following queries. 1. update ith value to X. 2. Find number of subarrays betweeen L and R, whose maximum values lie between L and R. (both inclusive)

Solution

One basic formula. (very basic)

let function c denote c*(c+1)/2 (The number of all the possible contigious subarrays from an array of length c.)

1+2+3+4+5 ... (N-1) + N = N(N+1)/2

Now, take L = 1, R = 10 and given array 2 0 11 3 0 (example given in problem)

(I'm directly taking an array instead of a series of updates to explain it).

Required subarrays between 1 to 5 are {1, 1}, {1,2},{4,4} and {4,5}

An interesting thing to observe is that ans = c(2)-c(1)+c(2)-c(1) (I'll explain how i came up with this.)

Two Facts: 1. Any element > R is never included in any subarray (like element 3). 2. Any number of elements smaller than L can be included in subarray as long as there is atleast one single element between L and R inclusive.

So, we are going to get 25 points first using this fact.

See this solution for details. in this solution, inc means consecutive elements till now which are smaller or equal to R, and exc means all consecutive elements < L till current position. Whenever we reach an element >= L, subtract excluded subarray count ( c(exc) ) from count and set exc = 0 and inc++ and whenever u get an element > R, add c(inc), subtract c(exc) and set both to 0. otherwise inc++, exc++.

Ans is count + c(inc)-c(exc). Got 25 points. This solution runs in O(QN) time.

I hope this logic is clear. Because if it isn't, be sure to read again once, twice, 10 times, 10^2 times, 2^ 10 times (I like this quote :P).

Now, Getting 52 points isn't difficult if You have heard about square root decomposition. I have submitted a solution using this technique too. :P. (I submitted too many solutions for this) I used in this solution apart from the counting technique we discussed above and one thing mentioned below

Cheers, now we got 52 points with this ease, but no longer. Problem setters aren't going to gift 52 points with this ease.

Now, think here, what information about a segment L to I and a segment from I+1 to R we need to find out all required information.

Refer to my solution (One more solution :P) alongwith to understand what's going on.

Let me help u. You need 8 variables (too much u feel i guess), as follows: 1. count => The count of subarrays already included in range, except those at borders. 2. incL => Number of elements from left to leftmost element which is > R. (0 if there's no element > R in range) 3. incR => Number of elements from right to rightmost element which is > R. (0 if there's no element > R in range) 4. excL => Number of elements from left to leftmost element which is >= L. (0 if there's no element >= L in range) 5. excR => Number of elements from right to rightmost element which is >= L. (0 if there's no element >= L in range) 6. size => size of range 7. found1 => boolean, which tells whether range contains atleast one element > R. 8. found2 => boolean, which tells whether range contains atleast one element >= L.

Any ideas how we are going to merge ranges?, it's simple enough.

Consider array 2 0 1 11 3 0 5

Answer of this Problems is c(3)-c(1)+c(3)-c(1) = 6-1+6-1 = 10

Think of this problem in two parts. for elements > R and for elements >= L.

For first part, consider any element > R as dividing element. for above example, 11 is dividing the total ranges into two sub-ranges of length 3 each.

For second part, consider any element >= L as dividing element. For above example, 2,1,11,3 and 5 are dividing elements, resulting in 2 ranges of length 1. ( {1,1} and {5,5} ).

If you understood this part, You can divide the given problem into two parts, the one dealing with elements to be included, and the one dealing with elements to be excluded.

Here comes the Main part of solution,The Segment tree. Now, as you may see, i have used an iterative segment tree,(I messed up recursive one and also, iterative is slightly faster if u take the trouble to understand it) about which you may read here. I first of all, created a class S (struct equivalent in java) which hold all this info about each segment of tree.

Now, the most important thing is to create a merge function, which will merge two segments into a larger one correctly.

You may see from my code, i have dealt with inclusion and exclusion separately, making my code simpler.

For first part, i check if both sides have element > R (our dividing element) (using boolean found1). if both has, include Left of large range will be outL of left segment and include right will be includeRight of right segment. count will be increase by c(left.incR + right.incL) because they are no longer boundary elements of segment.

In case only one segment has dividing element, incL and incR of output range is assigned accordingly.

Same way for large. And Here we go. We have solved the problem. Bet you didn't realize that.

All that is left to implement it. And Now, nothing is going to stop you from 100 points except a TLE in one file. (Not Sure, because i had use the following tip to save time.)

Link to My code.

PS: This was my first editorial using segment trees. So, i am sorry if any error might have crept in (without my knowledge, of course) Do give your review for this editorial.

As always, i wholeheartedly invite your suggestions and thank for your response to my previous editorials.

PS:Sorry for delay, was held up in something important. Delay gift will be posted as soon as I learn the technique of problem Polynomial. :D Hope you don't mind delay in delay gift. :D

Problem Link

Practice

Contest

Author:Azat

Tester:Pawel Kacprzak and Misha Chorniy

Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Tries, State Transitions

Problem

You are given a list of websites, some of which are blocked. You need to find a set of prefixes such that each of the blocked websites are recognised by some prefix but none of the non-blocked websites are. The aim is to minimise the sum of the length of the prefixes found.

Quick Explanation

Build a tries of the words, storing information regarding the words, their type (blocked or non-blocked). Use transitions during the traversal of trie (dfs) to find the optimal answer, if it exists.

Explanation

First of all, the problem deals with prefixes. Generally, problems on strings related to prefixes can be solved using hashing or trie. We will use trie to solve this problem.

Before starting to solve the problem, like what kind of data structure we would require and what information it should store, let us first analyse when the solution exists or not. The solution will not exist only when the blocked site is a prefix of a non-blocked website.. In all other cases the solution will exist because in the worst case, we might select the whole word for all the blocked websites.

Now, suppose the solution exist. We would like to minimise the total length of the selected prefixes. Now, since the length of one prefix is independent of the other, the total length would be minimum when we minimise each prefix selected. For minimising each prefix selected, we just want to selected the first character which differentiates between 2 blocked and non-blocked websites. Such a letter will exist as otherwise the solution would not have existed.

Let us understand this through examples. Let the blocked website be "codeforces" and allowed website be "codechef". Now, the $5^{th}$ letter ("f" vs "c") is the one which differentiates the 2 websites. Let the blocked website be "bing" and allowed website be "google". In this case, the $1^{st}$ letter will only differentiate the 2 websites. Let the blocked be "cs" and allowed website be "csacademy". In this case the solution will definitely not exist. As all the prefixes, "c" and "cs" would block both the websites.

From the examples, above our data structure should be able to handle 2 type of operations. They are :

1. Detecting whether the blocked website is a prefix of any non-blocked website.
2. Finding efficiently the first point of difference between 2 websites names.

Doing this through brute force will take complexity $O(\sum_{i=1}^{i=n} \sum_{j=i+1}^{j=n} min(L_i, L_j)$, where $L_i = $ length of string $i$. This is because the comparison between 2 strings to do the above operations can be done using a simple for loop, which terminates in worst case when either of the string to be processed finishes. In the worst case, it will be quadratic in the sum of length of strings given. Thus, it will only be able to solve subtask 1. For the complete solution, we use tries and store the following information in it to be able to handle above operations efficiently.

1. State 0 = no websites.
2. State 1 = non-blocked websites only.
3. State 2 = blocked websites only.
4. State 3 = both blocked and non-blocked websites.

After building of the trie, we just do a traversal (dfs) on it. Now, few things should be noted. Whenever we are in state $3$, we can go to state $\{0, 1, 2, 3\}$ in the child node. When we are in state $1$, we can only go to state $\{0, 1\}$ and when we are in state $2$, we can only go to $\{0, 2\}$ in the child node. This information will be enough to be able to handle above operations. Below are the claims for it :

1. Whenever, we make have a node at state $3$ and all of its children have state $\\{0, 1\\}$ only, we see that a blocked website is a prefix of a non-blocked website. Thus we should terminate our search here and claim that it is "impossible" to constrict an answer.
2. Otherwise in all cases, the solution exist. To find the minimal length, whenever we see that a state $3$, has a child with states $\\{0, 1, 2\\}$, we are sure to have found a point of difference between the blocked websites and non-blocked websites. This is when we should stop are search together on this current branch and add the required prefix to our solution.
3. Otherwise, the whole search space would only consist of wither blocked or non-blocked websites. This is easy as non-blocked website are not required to be searched. Also, for blocked websites, the $1^{st}$ character would only differentiate between the blocked and non-blocked website and thus we can terminate the search here too.

All the above operations can be done in $O(\sum_{i=1}^{i=n} {L}_{i})$, where $L_i = $ length of string $i$. This is because the trie can be build in above complexity and can be traversed in above complexity too.

If you had some other logic/algorithm to solve the above problem, feel free to discuss below

Time Complexity

$O(\sum_{i=1}^{i=n} {L}_{i})$, where $L_i = $ length of string $i$

Solution Links

Setter's solution

Tester's solution

Editorialist solution

Problem Link

Practice
Contest

Setter:Hasan Jaddouh
Tester:Amr Mahmoud
Editorialist:Bhuvnesh Jain

Difficulty

EASY-MEDIUM

Prerequisites

Strongly Connected Components, Bfs / Dfs

Problem

Find the minimum number of cells to select in a matrix so that we can reach every cell from it through a series of moves which is, "You can move from one cell to another only if they are adjacent (i.e. share a side) and the height of destination cell is not more than height of current cell."

Explanation

The edges in the graph will be between cells $(i, j)$ and $(x, y)$, only if they share a side. Also, the edges will be directed as the edge exists from a cell into another only if the height of destination cell is not less than the height of the current cell.

For example in the sample input 1, the edges will be as follows:

Now given a directed graph, we want to select a set of cells so that all cells are reachable from it. The first observation is 2 decompose the graph into Strongly connected components, as there may be cycles in the graph. This is because all the vertices in a cycle can be visited by starting from any vertex.

Now, we have a directed graph in which there are no cycles. (It is also called a DAG). In this graph, we claim that we chose only vertices with indegree $0$ to be in our set as the possible candidate solution.

Reason : Let us say there is an edge $P$ to $Q$ in the DAG. Let us denote the set of vertices reachable from $Q$ to be $S$. Then all vertices in $S$ are also reachable from $P$. But $P$ is not reachable from $Q$. So continuing this process, we will see that only vertices having indegree $0$ are not reachable from any other vertex but they as a set cover all the vertices reachable from it.

The DAG of input sample 1 is give below:

In the above figure, $1$ represents the set ${1}$, $2$ represents the set ${2,3}$, $3$ represents the set ${4,7}$ and $4$ represents the set ${5,6,8,9}$.

Thus, the algorithm is as below:

1. Construct the directed graph from the grid. Complexity is $O(N * M)$. Also, the number of edges in the graph is bounded by $(8 * N * M)$ as each cell can have at most 4 neighbors and it can have edge in both directions.
2. Decompose the graph into one with no cycles. You can use Tarjan's algorithm or Kosaraju algorithm for this step.
3. Find the number of vertices with indegree $0$ in DAG.

Author's Solution

The solution counts the number of components having same heights, such that all adjacent components are less (strictly) than it.

Proof: Each such component consisting of all cells of same height can be represented by 1 cell only. Now, each component can either have all adjacent components less tha it or not. If all cells adjacent to it are smaller, the those can be reached from the current cell, so they are ot counted towards the answer. If we repeat this process, for each component, we are bound to find only those cells which will contribute to the answer. Also, if we assume some cell that shouldn't be in answer was counted by above process, the it would contradict the fact that all adjacent components are lesser than it.

The above process can be simply implemented by a dfs call from every vertex and check if all components adjacent to it are smaller than it or not. For details, refer to author's solution.

Time Complexity

$O(N * M)$, per test case.

Space Complexity

$O(N * M)$

Solution Links

Setter's solution
Tester's solution
Editorialist's solution

I don't know much about threading. I just want to ask does using threading technique make our solution faster.

@vijju123@utkarsh1997

I'm trying to fill the already created linked list by traversing the linked list and then fill each node data with the user input but for some reason after 1040 times it stops asking further values. However let's say I have link list of size 1000 it will work just fine but for more than size of 1040 It doesn't prompt the user. I'm not entering value each time I generated random 1100 elements which I'm copying to the console.

inline void myArray<T>::init() {
 Node<T>* temp = head;
T input;
    while(temp!=NULL) {
    cin >> input;
    temp->data = input;
    temp = temp->next;

}
}

If I do something like this, it works just fine doesn't matter what the size of link list is..

inline void myArray<T>::init() {
 Node<T>* temp = head;
    while(temp!=NULL) {
    temp->data = 5;
    temp = temp->next;

}
}

So, Now I'm thinking the error has something to do with the input taking

//Developer : ruhul1995 || Time : 00:58 AM ||Date : 23/11/2017 //how to optimize this code..... i want the program to execute value of 10 power 6 and give the value for fibanacci and factorial...please help

include<iostream>

define MOD 1000000007

using namespace std; const int MAX = 2 * 1000000;

long long int f[MAX] = {0};

long long int fib(long long int n) { / Declare an array to store Fibonacci numbers. /

long long int f[n+1]; long long int i;

/ 0th and 1st number of the series are 0 and 1/ f[0] = 1; f[1] = 1;

for (i = 2; i <= n; i++) {

  f[i] = f[i-1] + f[i-2];

}

return f[n]; }

long long int fact( long long int n) {

if(n == 0 || n == 1)
    return 1 ;

else
    return n*fact(n-1);

}

int main() {

int testcase;

cin>>testcase;
while(testcase--)
{
    long long int n , m , k1 , i , p = 0 , final_answer = 0  ;
    cin>>n>>m>>k1;
    for( i = n ; i <= m ; i++)
    {
        p += fib(i) * fact(i) ;
    }

  //  cout<<"p="<<p<<endl;

    final_answer = p/k1 ; // x * k <= p

    cout<<(final_answer % MOD)<<endl;
}
return 0;

}

Can anyone take a look on my code? It gives me correct output, no idea why codechef says W/A. I was tring my best to make this code readable. Thanks!

Cutting Recipes Problem Code: RECIPE

It's Python 3.5.

Links:Problem /code

Hello guys! Could you please tell me what's wrong with my code? It looks to work well, but CodeChef says my answer is wrong.Thanks!

My solution / Problem link

i am unable to understand author's solution

link to the problem:-https://www.codechef.com/problems/IPCTRAIN

here is the author's solution:-https://s3.amazonaws.com/codechef_shared/download/Solutions/JULY17/Setter/IPCTRAIN.cpp

the part i am unable to undrstand is

   for (auto it: persons)
 {
 int lec = lectures[it.second];

        for (int i = 0; i < lec; i++) {
            auto iter = daySet.lower_bound(startDay[it.second]);
            if (iter == daySet.end()) {
                break;
            } else {
                lecturesTaken[it.second]++;
              daySet.erase(iter);
            }
        }
    }

what is this part doing

Hello Coders,

Hope you are having a great time coding hard. Here I present to you a Utility tool - StopStalk which will encourage you to keep your algorithmic progress going by coding with your friends and improve.

It retrieves your friends’ recent submissions from various competitive websites (CodeChef, Codeforces, Spoj, HackerEarth, HackerRank and UVa Online Judge for now) and shows you in one place. It includes lots of other features like - User streak notification, Global Leaderboard, Filter submissions, search problems by tags, Trending problems across these sites, Unified Todo list, View/Download submissions directly, cool analytics graphs and a lot more…

You can add friends who are already on StopStalk or you can also add a Custom User and start coding collectively by keeping a close watch on your algorithmic progress as compared to that of your friends.

If you want to increase your Custom User limit, you can share your StopStalk handle and you can get 1 extra user for every 3 users who register with your handle as Referrer's StopStalk handle.

Register here - StopStalk

The goal is to involve more and more people to Algorithmic Programming and maintain their streak. Also the project is completely Open Source - Github

Feel free to contribute. :)

We would be happy to hear from you - bugs, enhancements, feature-requests, appreciation, etc. In the end - Stop stalking and start StopStalking! Happy coding!

EDIT: 5100+ users already registered globally :) (Thanks a lot guys for your love!)

PROBLEM LINK:

Chef and his software

Author:Yogesh Malpani
Editorialist:Yogesh Malpani

DIFFICULTY:

MEDIUM.

PREREQUISITES:

ArrayList, Binary Search, Heap

PROBLEM:

Given the values of N transactions, the task is to insert these to records and print the value of Kth highest transaction in the records at each insertion.

QUICK EXPLANATION:

Find the index for the each new transaction using efficient Sorting algorithms which work well on an almost sorted list. Next find the Kth highest transaction and print it.

EXPLANATION:

How to process a new transaction of record, Ni?
For every Ni, check if it is smaller than current Kth largest element.
If yes, then ignore it. If no, then a modification of Binary Search can be used to find the index for the Ni. This can be done in O(LogN) time.
The transaction value is added at an index in the ArrayList which runs in amortized constant time, O(N) time.
So the Time complexity of processing a new transaction is O(N + LogN).
The Kth highest transaction is found in the ArrayList in constant time, O(1).

ALTERNATIVE SOLUTION:

Another Solution is to use Min Heap of size N to store N largest transactions of records. The Kth highest transaction is always at root and can be found in O(1) time.
How to process a new transaction of record?
Compare the new transaction value, Ni, with root of heap. If Ni is smaller, then ignore it. Otherwise replace root with Ni and call heapify for the root of modified heap. Time complexity of finding the Kth highest transaction is O(LogN).

AUTHOR'S SOLUTION:

Solution can be found here.

PROBLEM LINK:

Practice
Contest

Author:Trung Nguyen
Tester:Oleksandr Kulkov
Editorialist:Oleksandr Kulkov

DIFFICULTY:

CAKEWALK

PREREQUISITES:

None

PROBLEM:

You're given two numbers. Sum them up without carrying.

QUICK EXPLANATION:

Just do what is written in statement.

EXPLANATION:

One of possible codes to solve the problem:

    int a, b;
    cin >> a >> b;
    vector<int> A, B;
    while(a) {
        A.push_back(a % 10);
        a /= 10;
    }
    while(b) {
        B.push_back(b % 10);
        b /= 10;
    }
    while(A.size() < B.size()) A.push_back(0);
    while(B.size() < A.size()) B.push_back(0);
    for(int i = 0; i < A.size(); i++) {
        A[i] += B[i];
    }
    int ans = 0;
    reverse(begin(A), end(A));
    for(auto it: A) {
        ans = ans * 10 + it % 10;
    }
    cout << ans << endl;

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution can be found here.
Tester's solution can be found here.

RELATED PROBLEMS:

Problem Link

Practice

Contest

Author:Bhuvnesh Jain

Tester:Bhuvnesh Jain

Editorialist:Bhuvnesh Jain

Difficulty

MEDIUM

Prerequisites

Recursion, Bitmasks, Dynamic Programming.

Problem

Find the minimum time taken to cross the river by $N$ people if we can allow almost 2 people to use a boat such that the rowing time is equal to the minimum of the rowing time of both the people. Note that, slowing rowing time is given by larger integers.

Explanation

First of all, any type of greedy algorithm will only pass the first subtask and not any other. As the constraints are small and greedy solution will not work, we will try to come up with a dynamic programming solution.

Let us assume we denote the side where all the persons are initially standing by left and their destination, i.e. where they want to reach by right.

The first observation is that we will always try to send 2 people in the boat. This is because the slower person rowing time will then not contribute to the answer. The next observation is that once few people have crossed the river and reached "right", the boat will be brought to the left side by the person whose rowing time is the minimum among the persons at the right side. Next is that we can represent each person by a "bit-mask". The "left" and "right" bitmask denote that if the ${i}^{th}$ bit is one, then the ${i}^{th}$ person is present there else he is not present. The last observation is that the person can be present either in the "left" side or "right" side, not both ways. Thus, we only care about "left" side masks. The "right" mask can be calculated from the "left" ones, by setting the bits to 1 which are not present in "left".

With all these observations, we try to build a recursive solution as follows: (in the code, "turn" means, whether we send people from right to left or reverse)

//call with recurse((2^n)-1, 0) void recurse(LEFTMASK, turn): if (LEFTMASK == 0): return 0 //we transferred all the people RIGHTMASK = ((2^n)-1) ^ LEFTMASK if (turn == 1): //we want to transfer people to the left min_row = infinity, person = -1 for i in [0 .. n-1]: if (RIGHTMASK & (2^i)): if (min_row > row[i]): min_row = row[i] person = i return row[person] + recurse(LEFTMASK ^ (2^person), turn ^ 1) else: //we want to transfer people to the right if (number of set bits in LEFTMASK == 1): //only 1 person is left) for i in [0 .. n-1]: if (LEFTMASK & (2^i)): return row[i] + recurse(left ^ (2^i), turn ^ 1) else: //try every pair of people by sending them to right) ans = infinity for i in [0 .. n-1]: for j in [i+1 .. n-1]: if ((LEFTMASK & (2^i)) && (LEFTMASK & (2^j)): val = max(row[i], row[j]) val += recurse(LEFTMASK^(2^i)^(2^j), turn ^ 1) ans = min(ans, val) return ans

To optimise the above code for the full score, we can use dynamic programming so that each state is visited only once. This is also known as "top-down DP" or "recursion with memoization".

Time Complexity

$O(2^N * N * N)$

Space Complexity

$O(2^N)$

Solution Links

Setter's solution