I am done writing the code. And I am not sure if my program works correctly or not. How do I go about testing it?

It is a sincere request to Codechef to please provide editorials for other contests that are hosted on its platform. Currently, hardly any contest other than Long contest, Cook Offs and Lunch Time have editorials and other contests do not have any editorials. If someone like me just solves problems in the contest and then is not able to upsolve them, it will hardly improve my performance. This is a big discouragement for me and so I am not able to participate in more contests on Codechef. I know its not easy writing editorials for contests but if Codechef could provide some incentives for writing quality editorials or if some other solution could be found to this problem, it would be of great help to programmers like us.

There is no doubting the quality of questions that are there on this site. But if someone is unsuccessful in solving some problem, he would like to know how to solve it, and only then his coding abilities will improve else he would be discouraged from solving problems on codechef.

Thanks.

PROBLEM LINK:

Practice
Contest

Author:Praveen Dhinwa
Tester:Utkarsh Lath
Editorialist:Balajiganapathi Senthilnathan
Russian Translator:Sergey Kulik
Mandarian Translator:Gedi Zheng

DIFFICULTY:

Easy

PREREQUISITES:

Greedy

PROBLEM:

Given a string $s$, can you rearrange it such that no two consecutive characters are equal? If yes, print any such rearrangement.

SHORT EXPLANATION

We will use the following greedy algorithm. At each position, the character we are going to put will be the one with highest frequency and is not equal to previous character.

In other words, count the frequency of each character. For each position, select the highest frequency character which is not equal to the previous character. Decrement the frequency of this character. If such a character does not exist for any position, then a rearrangement is not possible.

EXPLANATION:

First we note that only the count of characters in the string $s$ matters i.e. the initial order of characters in the string $s$ does not matter.

Let us try to build the string from left to right. Intuitively, we want that the remaining highest frequency of the characters should be as low as possible (i.e. if a character has very high frequency, then it is tough for us to accommodate the no two consecutive equal characters condition).

So, for each position we will try to place the character with highest frequency such that it is not equal to previous character. If we have put all the characters in such way, then we are done. Otherwise we can prove that the arrangement is not possible and we output -1.

Time Complexity:

$O (n)$

Author's Solution

Let us take a string $s$ = "abbcc". Now, in this example, we have a bad space between the two b's and between the two c's. In the corresponding string "ab-bc-c", bad spaces are denoted by "-". Formally, we define number of bad spaces as number of places where we should insert some character different from it's previous and next one to make sure that string is valid.

Now, let us take most basic case for which it would be impossible to arrange the characters in the desired way. If the higest frequency character has size more than half of size the string, then it is impossible to construct the valid string because number of bad spaces by putting highest frequency frequency will be at least $\lceil \frac{n}{2} \rceil$.

Let us take the characters from in decreasing order of their frequency. Initially, we take the first character and put all its occurrences linearly. So, it we have total $k$ characters, we will have $k - 1$ bad spaces initially. Now, iteratively, we will reduce number of bad spaces. Now, we will take the next character and by using it, first we will first greedily remove as many bad spaces as possible. Now, if all the bad spaces are removed, then, we will try to create least amount of bad spaces as possible. Note that this process will reduce number of bad spaces strictly. As, you are processing characters one by one, and for a fixed character, you can have at most $\mathcal{O}(n)$ time. So total time will be $\mathcal{O}(26 * n)$ which will fit in the time. Please see author's solution from for more details.

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Praveen Dhinwa
Tester:Utkarsh Lath
Editorialist:Balajiganapathi Senthilnathan
Russian Translator:Sergey Kulik
Mandarian Translator:Gedi Zheng

DIFFICULTY:

Easy

PREREQUISITES:

Basic Graph

PROBLEM:

For a birthday party, $n$ persons can be invited. The $i$-th person gives Rs. $r_i$ (can be negative too, in case, you have to give that person $|r_i|$ rupees) as gift but requires that $f_i$ th person must also be present. What is the maximum amount of money that can be earned from the gifts.

SHORT EXPLANATION

Build a graph with $n$ nodes. There is an edge from $f_i$ to $i$ for all $i$. Note that this graph only consists of a number of components each having a simple cycle with possibly a few simple paths going out from it. For each component, we sum the values of all gifts in the cycle and do a dfs away from the cycle. For each path from the cycle, if the sum of values is positive, we add the value to the total value of the component. If the total value of the component is positive then we can add them to our answer otherwise we won't invite anyone from this component.

EXPLANATION:

Consider a graph with $n$ nodes corresponding to the $n$ persons. We add a directed edge from $f_i$ to $i$. What this means is that, if there is an edge from $a$ to $b$, then we have to invite person $a$ if we want to invite person $b$. Also, if we have invited a person $x$, then we can potentially invite all those nodes which have an incoming edge from $x$. Note that in this graph, each node has exactly one incoming edge. An example graph is shown below for input

11
2 0
3 0
2 0
3 0
6 0
8 0
6 0
7 0
6 0
5 0
5 0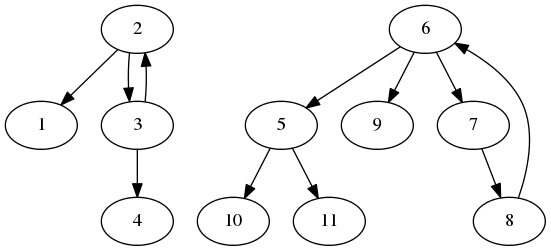

If we draw such a graph for a few examples, we will find a pattern in the graph: the graph is made up of a number of (weakly connected) components each of which has exactly one simple cycle and possibly few paths going out from the cycle. Let us formally prove this observation. Suppose there is a component which does not have any cycle, then there must be a node which does not have any incoming edge - a contradiction.

To proceed we observe that inviting a person in one component does not affect our choices in another component. Thus, we can calculate the maximum value we can get for each of the components one by one and sum them up.

Let us see how we can solve for a particular component. First note that if we are to invite anyone from this component then we have to invite everyone from the cycle. So, we sum the values of all nodes in the cycle. We can now consider this cycle as a single node having this value. So, now we have to determine the maximum value we can get.

Here is the important observation: if for a node $x$, we have invited some people who require node $x$ to be invited directly or indirectly, then the sum of the values of these people have to be non negative. Because otherwise we can exclude these people from the party and have a better total amount. This gives us an idea for the algorithm: for each node $x$, we solve recursively for each of its children (i.e nodes to which there is an outgoing edge from x). We invite a children only if we can get a positive value after inviting it. Finally, we sum up all such values from the children and add the node's own value to this sum. If this total value is positive then we can return it else it will be better to not invite $x$ or anyone who depends on $x$, so we return 0.

For each component, we call the above procedure starting from the cycle node and add the answer we got for all the components to get the total gift amount.

Implementation Notes
Now, how can we find the cycle corresponding to a single connected component? First note that, we just have to find a single vertex lying in the cycle, then we will go from $i$ to $f_i$ and so on and thus we will find the entire cycle.

So, for finding a single vertex lying in the cycle, let us construct a graph $G$ of $n$ nodes where edges are from $f_i$ to $i$. Now, pick any vertex in the component and keep taking the only outward edge in the graph. Finally, in the end, you will reach one vertex which surely lies in the cycle.

Time Complexity:

$O(n)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Anil Kishore
Tester:Utkarsh Lath
Editorialist:Balajiganapathi Senthilnathan
Russian Translator:Sergey Kulik
Mandarian Translator:Gedi Zheng

DIFFICULTY:

Medium-Hard

PREREQUISITES:

Meet in the middle, Tries

PROBLEM:

Given a $n \times n$ grid with values in each cell, if the energy of going from top left corner to bottom right corner is the bitwise xor of all the values in path, find the maximum energy. From a cell, you can go to either right or down in a single step.

SHORT EXPLANATION

Use meet in the middle approach. Use the anti diagonal of the grid as the middle. From start cell, enumerate all possible ways to reaching an anti diagonal cell. Add the energy for the path to a trie corresponding to that anti diagonal cell. Do the same for all paths starting from the target cell. For each anti diagonal cell, calculate the maximum value of xor of a path through the cell using a trie. The answer is maximum among all the anti diagonal cells.

EXPLANATION:

Section 1

Enumerating all possible paths from start to the target cell will time out. So, we use a clever way of reducing the time complexity called meet in the middle.

Suppose for a particular cell, we know all the xor values possible by starting from the start cell and reaching the cell (include the value of the cell too in the xor). Also, we additionally know the xor values for all possible paths from target to the cell (excluding the value of the cell). Now we can calculate the maximum energy path going through this cell using the approach discussed in Section 2. For now let us focus on which cells we need to consider. We need to select a group of cells for which we want to apply this approach. This group needs to satisfy the following 2 criteria:

1. All possible paths should go through at least one of the cells from the group
2. The number of possible paths from start to this group and from target to this group should be equal (to minimize the amount of work done).

The anti diagonal i.e. all cells $(i, j)$ satisfying $i + j = n + 1$ is perfect for this. As, 1. All paths from start to target has to go through an anti diagonal cell and 2. The path length of any path from start to the anti diagonal is $n - 1$ and from target to diagonal is also $n - 1$. So the amount of paths from start and target to the anti diagonal is equal. Note the forward diagonal $(i = j)$ is also fine.

Section 2

So for each cell we want to find the maximum energy path through that cell. Let us solve the following equivalent problem:

We are given 2 groups of values of size $n_1$ and $n_2$. We need to find the maximum $x_1 xor x_2$ where $x_1$ is taken from the first group and $x_2$ is taken from the second group.

A bruteforce approach with complexity $O(n_1 * n_2)$ will won't do as this will mean the complexity of the above algorithm will not be better than the bruteforce one.

The solution to this problem uses tries. We won't go into the details of what is trie. The following discussion assumes you know what a trie is and how to use it.

For one of the group we will build a trie by assuming the number as a fixed size bitstring of length 31. Insertions into the trie will proceed from the msb to lsb i.e. from bit #30 to bit #0.

So now we have a trie of one of the group. Now for each value in the other group, we will find what is the maximum xor value for this value.

Let us start from the msb. Now we want the msb to be 1 if possible. Xor of two bits is 1 if they are different. So, if the msb of the current number is 1, we will see if there is a 0 in the trie at the root. If the msb of the number is 0, we will look for 1 in the root. If the bit is present in the root i.e. there is a child node corresponding to that bit, then we will keep the msb bit of the answer as 1 and search recursively for the next bit. Otherwise, we can only have 0 in msb, so we keep the msb as 0 and search recursively for the next bit using the child of the root corresponding to the bit. We continue this till we reach bit #0 when we get the maximum value.

We do this for all $n_2$ values and return the maximum. This takes $O(n_1 + n_2)$ time which is much better than $O(n_1 * n_2)$. This is the reason the meet in the middle approach will work within time limit.

We do the above procedure for all anti diagonal cells and the answer will be the maximum among them.

Time Complexity:

Note that all the paths are of length $n$ from the diagonal. At each step we can go right or down. So there are $2^n$ paths. Finding the maximum takes O(1) time. So overall complexity is:

$O(2^n)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Praveen Dhinwa
Tester:Utkarsh Lath
Editorialist:Balajiganapathi Senthilnathan
Russian Translator:Sergey Kulik
Mandarian Translator:Gedi Zheng

DIFFICULTY:

Hard

PREREQUISITES:

Geometry

PROBLEM:

Given $n$ points each with a positive weight, find the minimum weighted convex polygon with $k$ vertices chosen among the $n$ points. Do this for all $k$ from $3$ to $n$. The weight of a polygon is the sum of the weights of the points enclosed by it (including the boundaries).

SHORT EXPLANATION

Suppose we fix a point $p_1$ as the lower right corner of the polygon we are about to construct. We will sort all the valid points (i.e. those that are above $p_1$) in counter clock wise direction with respect to $p_1$. Now let us define $dp(p_3, p_2, k)$ as the minimum weighted polygon which has $p_1$ as the lowest point, $p_3$ and $p_2$ are the last two added points and we have to add $k$ more vertices. Now, for all vertices in counter clock wise order, we try adding each point $i$ which is to the left of the line connecting $p2$ to $p3$ and recursively solve the $dp(i, p3, k + 1)$ and add we also add the weights of the point inside the triangle $p2 - p3 - i$. We take minimum over all such $i$ and that will be the answer for $dp(p_3, p_2, k)$.

Now we try fixing each of the point as the lower most one (i.e. $p_1$) and do the above procedure. For each $k$, we take minimum over all such fixed points. We do this for all $k$ (3 \leq k \leq n) to get the final answer$.

EXPLANATION:

Let us fix a point $p_1$ as the bottom most point of the polygon (i.e. the one with the least $y$ coordinate). Since this is the bottom most point, we can ignore all the points which have $y$ values less than $p_1$. Now we sort the remaining points in counter clockwise direction. We want to get the minimum weighted convex polygon for each $k$ having $p_1$ as the bottom most point.

The key observation is that suppose we have a minimum weighted convex polygon with $k$ vertices, then if we remove any vertex, we will be left with a minimum weighted convex polygon of $k - 1$ vertices having $p_1$ as the bottom most point. So, to get the answer for $k$, we try adding each valid point as the next vertex and solve the problem for $k - 1$ vertices. Then take the minimum over all such valid points to get the minimum value for $k$ vertices.

In other words, we are building the polygon triangle by triangle. What other information are needed for implementing this?

1. We need to know the last two added points added to the polygon. This is to ensure that the next point we add does make a convex polygon (i.e it has to be to the left of the line made by the last two points).
2. We need to know the weight of all possible triangles. We can pre-calculate this in $O(n^4)$ time and $O(n^3)$ space. Let us define $totalWeightsInside[i][j][k]$ as the weight of the points inside the triangle formed by points $i, j$ and $k$. We can calculate this by looping through all points and adding its weight to $totalWeightsInside[i][j][k]$ if that point lies inside the triangle formed by $i, j$ and $k$.

Let the function $dp(p_3, p_2, k)$ return the minimum weighted convex polygon with $p_1$ as the bottom most vertex, $p_3$ and $p_2$ as the last two vertex and $k$ vertices remaining to be added. Now we loop through all valid points $i$ which are ahead of $p_3$ in counter clockwise order and see if can add $i$ to the polygon. We can add $i$ only if it is to the left of the line formed by $p_2 - p_3$. Otherwise the angle made by $p_2 - p_3 - i$ will be greater than 180 degrees and hence it won't be a convex polygon. Now to get the weight, we recursively solve for $dp(i, p3, k - 1)$ and add the weights of the points inside the triangle formed by $p_2 - p_3 - i$ to the weight. We try this for all $i$ and the minimum among them would be the answer. Finally note that for a fixed $p_1$, the state may repeat. So, we memoize the values to avoid recalculation.

For getting the final answer, we loop through all points and fix them as $p_1$. Then we store all the points which are not below $p_1$ and sort them in counter clockwise order. Now we have to select the next 2 vertices of the polygon. So we loop through all pairs of valid points and keep them as the next 2 vertices. Finally we need to solve for all $k$, so we will loop for $k$ from 3 to $n$ and call $dp(p3, p2, k - 3)$ to get the answer for this case. We keep updating the minimum weighted polygon for $k$ vertices using this value.

Please consult author's solution for the sample implementation of this idea.

Time Complexity:

$\mathcal{O} (n^5)$

• $\mathcal{O}(n)$ for fixing vertex $p_1$
• $dp(p_3, p_2, k)$ has total number of states equal to $\mathcal{O}(n^3)$ and total number of transitions equal to $\mathcal{O}(n)$. Hence, time taken will be $\mathcal{O}(n^4)$.
• Finally, the total time will be product of both, i.e. $\mathcal{O}(n^5)$

AUTHOR'S AND TESTER'S SOLUTIONS:

Author's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Konstantsin Sokol
Tester:Gedi Zheng
Editorialist:Miguel Oliveira

DIFFICULTY:

Easy.

PREREQUISITES:

Sets.

PROBLEM

Given 2 sets of integers, count the number of integers that appear in both sets and the number of integers between 1 and N that do not appear in either set.

QUICK EXPLANATION

The source files that are both tracked and ignored are the intersection of the two sets given in the input.

The source files that are both untracked and unignored are the numbers in the interval [1, N] that do not appear in either of the given lists.

EXPLANATION

We are given 2 lists of unique integers. We can treat these lists as sets. A set is a collection of distinct items (integers in this case).

Both ignored and tracked source files

The source files that are both tracked and ignored are the integers in the intersection of the 2 given sets.

To calculate the set intersection, the simplest way is to search all integers of the first set in the second set. Since we have only 100 numbers, we could do this search naively with 2 nested loops and a time complexity of O(M*K).

A smarter way is to use a hash table. Note that the numbers are between 1 and 100. We can use an array with 100 positions and mark position i if number i is in the set. This way we can look-up if a number is in a set in O(1) time. Thus, the time complexity of the set intersection is O(M) to build set A, O(K) to build set B and O(M) to check if the items in set A appear in set B. The total time complexity of this set intersection is O(M+K).

Also, you can use set, map, unordered_map in C++ to make a look up table too.

Also, sometimes you can use bitwise operations with bit packing the sets in the integer to int or long data type. Then, you can use bitwise operations (e.g. and, or, xor) to check set intersection. Also, for two sorted arrays a, b, you can use set_intersection in C++ to find number of common elements in both the arrays in linear time.

Both unignored and untracked source files

The number of source files that are both untracked and unignored are the integers between 1 and N that do not appear in set A or B. We can use the same logic and search all numbers between 1 and N in sets A and B. This will take O(N) time if we use hashing or O(N * (M+K)) with the naive search.

Time Complexity

The total time complexities are O(N + M + K) using hashing and O(M * K + N * (M+K)). Both were perfectly fine as the size of the sets are up to 100.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Konstantsin Sokol
Tester:Gedi Zheng
Editorialist:Miguel Oliveira

DIFFICULTY:

Easy.

PREREQUISITES:

Math, Linear Algebra.

PROBLEM

We have a system of N equations on N variables. Equation i is of the form: $x_1 + x_2 + ... + x_{i-1} + x_{i+1} + .. x_n = A_i$. You can prove that solution of this system of equations will be unique. You have to solve this system of equations.

QUICK EXPLANATION

• Write each equation in form of $sum - x_i = A_i$ where $sum$ denotes sum of all the variables i.e. $sum = x_1 + x_2 + \dots + x_n$. So, $x_i = (sum - A_i)$
• Now only thing that we have to do is to compute value of $sum$ in terms of known values $A_1, A_2, \dots A_n$.
  Let us add all the equations, we get $N * sum - ( x_1 + x_2 + \dots + x_n) = A_1 + A_2 + \dots + A_n$.
  As, $sum = x_1 + x_2 + \dots + x_n$, we get $sum = \frac{A_1 + A_2 + \dots + A_n}{N - 1}$
• So finally, $x_i = \frac{A_1 + A_2 + \dots + A_n}{N - 1} - A_i$.

EXPLANATION

The solution to a system of 2 variables is trivial:

$\begin{cases} x_2 = A_1 \\ x_1 = A_2 \end{cases}$

If we have 3 variables, the system is:

$\begin{cases} x_2 + x_3 = A_1 \\ x_1 + x_3 = A_2 \\ x_1 + x_2 = A_3 \end{cases}$

Each variable appears $N-1$ times. Let's sum these equations. We get

$\begin{array}{lcl} 2 * x_1 + 2 * x_2 + 2 * x_3 & = & A_1 + A_2 + A_3 \\ 2 * (x_1 + x_2 + x_3) & = & A_1 + A_2 + A_3 \\ x_1 + x_2 + x_3 & = & \frac{A_1 + A_2 + A_3}{2} \end{array}$

Now, to know the value of each variable, we can reuse the original equations. Then, to know the value of x1, we can use the fact that $x_2 + x_3 = A_1$. Let $S = A_1 + A_2 + A_3$, then $x_1 + A_1 = \frac{S}{2} \Leftrightarrow x_1 = \frac{S}{2} - A_1$.

In general, let $S = A_1 + A_2 + ... + A_n$. For each variable, $x_i = \frac{S}{N-1} - A_i$.

Time Complexity

We can compute the sum in linear time and calculate the answer in linear time as well for a $O(N)$ solution.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Konstantsin Sokol
Tester:Gedi Zheng
Editorialist:Miguel Oliveira

DIFFICULTY:

Medium-hard.

PREREQUISITES:

Dynamic Programming, Binary Indexed Trees.

PROBLEM:

You are given a sequence $a_1, a_2, ..., a_N$ of non-negative integers. Your task is to process Q queries of the following format: each query is described by two integers L ≤ R and asks to calculate the number of triples (i, j, k), such that $L  <  i  <  j  <  k  <  R$ and $a_L > a_i < a_j > a_k < a_R$.

EXPLANATION:

The first thing to notice is that there are repeating patterns in the subsequences. For example,

• Increasing subsequences like $a_i < a_j$ and $a_k < a_R$
• Decreasing subsequences like $a_L > a_i$ and $a_j > a_k$
• Triples $a_L > a_i < a_j$ and $a_j > a_k < a_R$

So, suppose we process the sequence from left to right. We can break down the triplets such that $a_L  >  a_i  <  a_j  >  a_k  <  a_R$, with $L < i < j < k < R$, in parts:

• For a fixed $R$, the number of subsequences $a_L  >  a_i  <  a_j  >  a_k  <  a_R$ is the number of subsequences $a_L  >  a_i  <  a_j > a_k$ such that $a_k < a_R$
• For a fixed $k$, the number of subsequences $a_L  >  a_i  <  a_j  >  a_k$ is the number of subsequences $a_L  >  a_i  <  a_j$ such that $a_j > a_k$
• For a fixed $j$, the number of subsequences $a_L  >  a_i  <  a_j$ is the number of subsequences $a_L > a_i$ such that $a_i < a_j$
• The number of subsequences such that $a_L > a_i$ is the number of integers between $L$ and $j$ below $a_L$

Hence, we can build up on the smaller parts in order to find the solution for each query.

We can use a binary indexed tree (BIT) to keep counts for each part

• BIT_r counts how many subsequences $a_L  >  a_i  <  a_j > a_k$ are there where $a_k$ equals a query value.
• BIT_k counts subsequences $a_L  >  a_i  <  a_j$.
• BIT_j counts subsequences $a_L  >  a_i$.
• BIT_i counts the frequency of integers seen so far.

Suppose we fix $L$ and process the elements from left to right until $N$. For each $x$ up to $N$,

• Use BIT_r to count the number of subsequences $a_L  >  a_i  <  a_j > a_k$ up to $x$, such that $a_k < a_x$. The answer to a query in interval [L, x] is this value. Save this in a table.
• Use BIT_k to count the number of subsequences $a_L  >  a_i  <  a_j$, such that $a_k > a_x$. Update BIT_r with this number.
• Use BIT_j to count the number of subsequences $a_L  >  a_i$, such that $a_j < a_x$. Update BIT_k with this number.
• Use BIT_i to count the number of integers such that $a_i < a_j$. Update BIT_j with this number.
• Insert $a_x$ to BIT_i

This pre-processing takes $O(N^2 log N)$ time because we do 4 inserts and updates in BITs for each valid interval $[L, R]$. After this pre-processing, we can answer any query using the computed table in $O(1)$ time. Thus, the total time complexity is $O(N^2 \log N + Q)$.

Implementation notes:

• Since the input numbers can be up to $10^9$, we should pre-process them and compress the values in a range $[1, N]$ (we don't care about the number itself, just their relative order)
• Instead of implementing separate Binary Indexed Trees for increasing and decreasing subsequences, we can just check for increasing subsequences. To do this, note that we can transform a decreasing subsequence into an increasing one by changing each value $a{_i}$ to $maxvalue - a_i$.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author:Konstantsin Sokol
Tester:Gedi Zheng
Editorialist:Miguel Oliveira

DIFFICULTY:

Hard.

PREREQUISITES:

Math, Linear Algebra.

PROBLEM

Given 2 polynomials Q and T, find a polynomial P such that $P(x) = Q(x) + \int_0^1 T(x \cdot s) P(s) ds$ holds for every real $x$.

EXPLANATION

We are given polynomials Q and T, and the formula $P(x) = Q(x) + \int_0^1 T(x \cdot s) P(s) ds$.

$Q(x) = \sum\limits_{k=0}^n q_k x^k$ and $T(x \cdot s) = \sum\limits_{k=0}^m t_k \cdot x^k \cdot s^k$

Thus, $P(x) = Q(x) + \int_0^1 T(x \cdot s) P(s) ds = \sum\limits_{k=0}^n q_k x^k + \int_0^1 (\sum\limits_{k=0}^m t_k \cdot x^k \cdot s^k) P(s) ds$

$P(x) = \sum\limits_{k=0}^n q_k * x^k + \sum\limits_{k=0}^m t_k \cdot x^k * (\int_0^1 s^k P(s) ds)$

Notice that $\int_0^1 s^k P(s) ds$ is a constant for each $x$. Let's call this $c_x$. Then, $P(x) = \sum\limits_{k=0}^n q_k x^k + \sum\limits_{k=0}^m t_k x^k \cdot c_x$

Now we are interested in finding all $c_1, c_2, ..., c_m$.

$c_i = \int_0^1 s^i P(s) ds = \int_0^1 s^i (\sum\limits_{k=0}^n q_k s^k + \sum\limits_{k=0}^m t_k s^k \cdot c_x) ds$

$c_i = \sum\limits_{k=0}^n q_k \cdot \int_0^1 s^{k+i} ds + \sum\limits_{k=0}^m c_k \cdot t_k \int_0^1 s^{k+i} ds$, note that $\int_0^1 s^{k+i} ds = \frac{1}{k+i+1}$

Then we have $c_i = \sum\limits_{k=0}^n q_k \cdot \frac{1}{k+i+1} + \sum\limits_{k=0}^m c_k \cdot \frac{t_k}{k+i+1}$

Thus, we have $m$ equations and $m$ variables. We can build a system of equations and use the gaussian elimination method to solve the system and calculate the coefficients.

Time Complexity

Building the system of equations will take O(N) time and the gauss elimination O(M^3), thus giving O(N + M^3) total time.

AUTHOR'S AND TESTER'S SOLUTIONS:

Setter's solution
Tester's solution

PROBLEM LINK:

Practice
Contest

Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey

DIFFICULTY:

Cakewalk.

PREREQUISITES:

Simulation of brute force algorithm.

PROBLEM:

You have a string $S$ which consists of $N$ uppercase English letters. You are allowed to at most once do the following process: Choose any position in the string, remove the character at this position and insert the same character back in any other place.

Find the lexicographically smallest string you can achive.

QUICK EXPLANATION:

Generate all possible strings, and keep track of the lexicographically smallest string.

EXPLANATION:

We can create all possible strings by removing a character at some position and adding it to other position. We will have one string for each removed and inserted positions. So overall there will be total $O(n^2)$ such possible strings. We can implement the process of removal and additions of character at some position in $O(n)$ time. Overall it will take $O(n^2 * n) = O(n^3)$ time.

We just need to write a function Modify(), which will take input two integers $i$ and $j$, and delete the $j^{th}$ character of the given string and insert it between $i^{th}$ and $(i+1)^{th}$ character. Modify() function will generate a new string which we can get by performing the given process at most once. We can run Modify() function on all possible values of $i$ and $j$, and report the minimum one.

Peseudo code can be given as below:

string lex_minimum = given_string;
for(int i = 0 ;  i< given_string.length() ; i ++)
{
    for(int j =0 ; j < given_string.length() ; j++)
    {
        temp_string = Modify(i,j);
        lex_minimum = min(temp_string,lex_minimum);
    }
}
print lex_minimum

Solving the given problem with better complexity is an interesting task, please comment if you find such solution.

Solution:

Setter's solution can be found here
Tester's solution can be found here

PROBLEM LINK:

Practice
Contest

Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey

DIFFICULTY:

Easy.

PREREQUISITES:

BIT, segment tree.

PROBLEM:

Determine minimum amount of minutes required to paint a fence consisting of $N$ parts, in green color. Each part is initially painted either red or green. We can chose an index $X$, and flip colors in range $[X,\min(X+K,N-1)]$ in one minute.

QUICK EXPLANATION:

Consider the index where first red is occurring as $T$, flip the colors in range $[T,\min(N,T+K-1)]$. Keep repeating this step until each part is colored green.

EXPLANATION:

First lets see how to solve the problem, later we can see the proof of correctness.

Consider the index at which first red is occurring and call it $T$, flip the colors in range $[T+\min(N,T+K-1)]$. Keep repeating the given procedure unless whole array is green. After each iteration value of $T$ will be increasing, so the given algorithm will terminate in less than or equal to $N$ steps.

Each iteration may take $O(N)$ amount of time, hence the given algorithm will be taking $O(N^2)$ time. As the $N$ can be $10^5$ in the given problem, we need to optimize our solution.

We can solve the problem in $O(N\log N)$ time. Range flip can be seen as adding $1$ to the range and value of color can be obtain using sum at that particular index modulo $2$. If the $\text{sum} \%2$ is $0$, then color at that index will be same as the initial one or flipped otherwise. The range updates and queries can be done in $O(\log N)$ time using BIT or segment tree.

O(N) Solution:

It can be done in $O(N)$ as well. Adding $1$ to range $[L,R]$ can be seen as adding $1$ to index $L$ and adding $-1$ to index $(R+1)$. When we want to retrieve the value at specific index, we need to take the prefix sum upto that index. See sub problem 1 of this editorial for more details.

Proof:

The given procedure can be proved correct using the following lemmas.

1. Order of the updates doesn't matter.
2. Starting index of any 2 updates will be different, as 2 updates at same starting position will cancel each other.
3. If we sort the minimum update sequence and suppose first update happens at index $i$, then at each index in range $[0,i-1]$ color must be green and at index $i$, color must be red.

Solution:

Setter's solution can be found here
Tester's solution can be found here

PROBLEM LINK:

Practice
Contest

Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey

DIFFICULTY:

Easy-Medium.

PREREQUISITES:

Counting, Dynamic Programming, Recursion.

PROBLEM:

Given strings $X$ and $Y$, count the number of strings of length $n$ which do not contain string $S (X \leq S \leq Y)$ of length $m(\leq n)$ as a substring.

EXPLANATION:

In this problem it is asked to count the number of strings of length $n$ which do not contain string $S (X \leq S \leq Y)$ of length $m(\leq n)$ as a substring. Let $H$ be a set of strings which are lexicographically in between $X$ and $Y$ inclusively that is $H = \{S : |S| = m \wedge X\leq S \leq Y \}$. Now define $\text{dp}[i]$ as the number of strings of length exactly equal to $i$ which do not contain string(s) which belong(s) to $H$ as a substring. It is clear that if $i < m$ then $\text{dp}[i] = 26^i$.

For $i \geq m$, define a recursive function $f(S, n, i)$ which takes input string s, ending index $n$ and index $i$ which is to be filled. This function returns the number of valid strings( which are not hated ) whose last $n-i$ letter are already fixed as $S$. For example $f(AB, 5, 3)$ will return number of valid strings of length 6(assuming zero indexing and $n=5$) whose last 2 letters are fixed as "AB". Also define a function $V(S, len)$ which return 1 if string $S$ of length $len$ is valid else it returns 0. Note that if $len < m$ then the string is trivially valid else we have to check $X \leq S \leq Y$. Further $len$ will always be less than or equal to $m$ by virtue of following definition of $f(S, n, i)$ where a value greater than $m$ is never passed to $V(S, len)$

Now $f(S, n, i) = 24\text{dp}[i] + f(AS, n, i-1)\times \text{V}(AS, \min(m, \text{len}(AS)) + f(BS, n, i-1)\times \text{V}(BS, \min(m, \text{len}(BS))$ because the ith index can be C-Z, in which case we are left with string of length $i$ (index $0$ to $i-1$) thats why the term $24\text{dp}[i]$; or ith index can be 'A' in that case we have to check whether the string from ith index to min(i+m-1, n) is valid or not thats why the term $f(AS, n, i-1)\times \text{V}(AS, \min(m, \text{len}(AS))$ and similar expression when ith index is 'B'. Base case will be when $i=-1$ in that case return 1.

Now, for $i \geq m$, $\text{dp}[i] = f(\text{empty string} , i-1, i-1)$. So, the final answer to the question will be $\text{dp}[n]$. Refer to the editorialist code in the solution section for more detail. The worst case time complexity of this algorithm is $\mathcal{O}(n 2^n)$.

Solution:

Setter's solution can be found here
Tester's solution can be found here
Editorialist's solution can be found here

PROBLEM LINK:

Practice
Contest

Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey

DIFFICULTY:

Medium.

PREREQUISITES:

Dynamic Programming

PROBLEM:

Given a set of integers $\{0, 1, 2, ..., n\}$, find the number of ways of choosing a subset of $k$ integers such that the xor of all chosen integers has exactly $B$ set bits(in the binary representation).

EXPLANATION:

In this problem, our approach will be to generate(smartly) all possible $k$ integers bit by bit from MSB in a particular order. At any step $i$ we will assume that we have generated $k$ integers upto ith bit following a order and extend it to i+1th bit( taking care of the ordering as well) and in the process, counting all possible ways of extension of $k$ integer. Now to smartly count all the ways we will use dynamic programming approach.

Define a 3-D dp matrix $\text{dp[i][b][mask]}$ which stores the number of ways of choosing $k$ integers of $i$ bits such that their xor has $b$ set bits and the $k$ integers follow a specific order according to the mask. Important idea to note here is that the $k$ integers chosen follow a specific order defined by mask as follows :-

0th bit of mask is 1/0 iff 1st chosen integer is strictly less/equal than n upto i bits from MSB.
1st bit of mask is 1/0 iff 2nd chosen integer is strictly less/equal than 1st chosen integer upto i bits from MSB.
2nd bit of mask is 1/0 iff 3rd chosen integer is strictly less/equal than 2nd chosen integer upto i bits from MSB.
.
.
.
k-1 th bit of mask is 1/0 iff kth chosen integer is strictly less/equal than k-1 th chosen integer upto i bits from MSB.

This means that the $k$ integers are considered in decreasing order. Since the ordering doesn't matter in set, there is no harm in generating $k$ integer in decreasing order. Lets say the first $i$ bits of $k$ integers are already generated according to mask. Now these $k$ integers can be extended to $i+1$th bit(from MSB) in $2^k - 1$ ways, that is the value of pred( it is a $k$ bit number such that $j$th bit of pred is $i+1$th bit of $j$th chosen number, refer to the figure below for more detail) can take $2^k - 1$ value. And for each value of pred and old mask the ordering of $k$ integer ( also the mask ) will change. Note that the newmask (which denotes the ordering among k chosen number) may be invalid because there may be some pair(s) of numbers which are not in decreasing order, in that case the newmask will be invalid. Now lets consider each possible scenario case by case.

First initalize newmask with mask. The first condition involves the number $n$ and the 1st chosen number.

If 0th bit of mask is 0 which implies 1st number is equal to n upto i bits from MSB then
Case 1.1: If i+1th bit of n is 1 and i+1th bit of 1st number is 0 then 0th bit of newmask will be 1 as 1st number is now smaller than n.
Case 1.2: If i+1th bit of n is 1 and i+1th bit of 1st number is 1 then no change in newmask.
Case 1.3: If i+1th bit of n is 0 and i+1th bit of 1st number is 0 then no change in newmask.
Case 1.4: If i+1th bit of n is 0 and i+1th bit of 1st number is 1 then in this case newmask will be invalid.

The following condition involves j+1th and jth chosen number where j varies from 1 to k-1.
If jth bit of mask is 1 that means j+1th number is strictly smaller than jth number upto ith bit and even if i+1st bit is 0 or 1 this order will not change hence in this case newmask will not change.
Else If jth bit of mask is 0, this means j+1th number is equal to jth number and depending upon the i+1th bit of those two number newmask will change.
Case 2.1: If i+1th bit of jth number is 1 and j+1th bit of 1st number is 0 then jth bit of newmask will be 1 as j+1th number is now smaller than jth number.
Case 2.2: If i+1th bit of jth number is 1 and j+1th bit of 1st number is 1 then no change in newmask.
Case 2.3: If i+1th bit of jth number is 0 and j+1th bit of 1st number is 0 then no change in newmask.
Case 2.4: If i+1th bit of jth number is 0 and j+1th bit of 1st number is 1 then in this case newmask will be invalid.

After the computation of newmask and it validity update the dp state dp[i+1][b+setBits(pred)%2][newmask] += dp[i][b][mask] if newmask is valid. Base case will be dp[0][0][0] = 1. Below is basic structure of the code for more clarity.

for(i = 0 to 31) for(b = 0 to B) for(mask = 0 to 2^k - 1) :
    for(pred = 0 to 2^k - 1) :
        (newmask, validity) = generateNewMask(mask, pred);
                              //this function generates newmask according to the above rules
        if(validity) dp[i+1][b+setBits(pred)%2][newmask] += dp[i][b][mask];
                              //setBits(x) return number of set bits in x

Now the final answer will be dp[31][B][2^k - 1] + dp[31][B][2^k - 2] corresponding to the case when 1st number is equal to n and when 1st number is strictly less than n. Refer to the tester's code for more details. The time complexity of the algorithm is $\mathcal{O}(B\log n2^k)$.

Solution:

Setter's solution can be found here
Tester's solution can be found here

PROBLEM LINK:

Practice
Contest

Author: Vitaliy Herasymiv
Tester: Istvan Nagy
Editorialist: Amit Pandey

DIFFICULTY:

Easy.

PREREQUISITES:

Simulation.

PROBLEM:

Given a robot and $N\times N$ grid, find any valid sequence of moves starting from $(1,1)$ such that there are no more than three consecutive turns that moved the robot in the same direction and robot covers each cell at-least once.

QUICK EXPLANATION:

Start at $(1,1)$ and at each step, consider two consecutive rows and visit in pattern $DRURDRU$(D=Down, R=Right, U=Up). Once both rows are done, jump to another pair of rows. Take care of hurdles using some specific technique. See explanation for details.

EXPLANATION:

There might be many possible solutions to the problem, lets discuss one of them. We need to derive an strategy which will be covering all of the cells using minimum number of steps and later we have to increase the steps to stop ourselves to go to forbidden cells.

Start at co-ordinate $(1,1)$, Consider two rows at a time. visit in the pattern $DRURDRU$.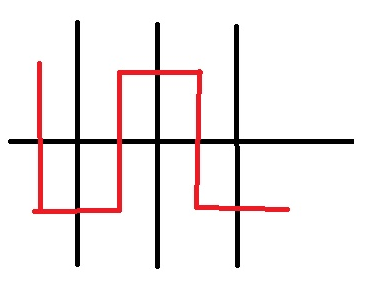

If in any row, we found a forbidden cell then it will fall in one of these two cases.

1. We are visiting in pattern $DRURDRU$. Suppose while we are going up after going right and get to a cell which is forbidden, then we may continue in right direction and then go up(the pattern $DRUR$ becomes $DRRU..$). See the first one in the image.
2. We get a forbidden cell while we are going into right and previous one was the up. In this case, we may go down again, go right twice and then go up($DRURDR$ becomes $DRUDRUR..$).

In second case, we are visiting a cell more than once but we are skipping a cell as well. So, number of steps will not exceed number of cells. So, if $N$ is even then in worst case we are using $O(N^2)$ number of steps. If $N$ is odd, we are using $(N-1)^{th}$ row twice so, we using $N(N+1)$ number of step in worst case.

While connecting the row pair ending we will be using at most $5$ steps while there is some forbidden cell, which can be shown using the following image. If there is no forbidden cell, we can do it in lesser number of steps.

Maximum number of step would be $\le N(N+1) + 5(\frac{N}{2}) = N(N+\frac{7}{2})$

It is easy to see we are never taking three steps in same direction in any of the case. In first two cases, we are taking at most two steps in the same direction. While we are switching the pair of rows, we are taking three steps in one direction in the same direction and later changing the direction just after third step.

Solution:

Setter's solution can be found here
Tester's solution can be found here

Hi,

There is a Getting started page on CodeChef which contains resources on competitive Programming and programming languages.

Check CodeChef-resources repository on Github.

It contains resources on:

• Get started on CodeChef Frequently
• Solve your first problem on CodeChef (video links)
• Competitive programming references
• Introduction to Competitive
• Programming Contests List of Topics
• Courseware: Video lectures
• Algorithms Lectures
• Algorithm Tutorials
• Wikibooks links
• Data Structures Algorithms C/C++ Java
• Python
• Linux

I request CodeChef Community to contribute to repo.

Please read Contributing to this repository before creating pull requests.

If you face any issue send an email to feedback@codechef.com.

PROBLEM LINK:

Practice
Contest

Author: Devendra Agarwal
Tester: Anudeep Nekkanti
Editorialist: Amit Pandey

DIFFICULTY:

Cakewalk.

PREREQUISITES:

Basic geometry, recursion.

PROBLEM:

Find the maximum number of squares of size $2\times2$ that can be fitted in a right angled isosceles triangle of base $B$. All sides of the square must be parallel to both base and height of the isosceles triangle.

QUICK EXPLANATION:

As $B<=1000$, we can pre-compute the output for all the test cases, and report the answer in $O(1)$ time for each of the query.

EXPLANATION:

First consider the right angle triangle $\Delta XYZ$, where $YZ$ is the base of triangle. Suppose length of the base is $B$. If we consider the position of first square with the vertex $Y$, we will have $(B/2 - 1)$ squares in the base, and we will be left with another isosceles right angle triangle having base length $(B-2)$.

Let $f(B)$ = Number of squares which can be fitted in triangle having base length $B$.

$f(B) = (\frac{B}{2} -1) + f(B-2)$

The given time limit is sufficient even if we calculate $f(B$) using the given recursion, and use memoization. Later we can answer each query in $O(1)$ time. We can do it for even and odd numbers separately with the base case $f(1) = f(2) = f(3) = 0$.

The given recursion can be solved in following manner.

$$ f(B) = \frac{B-2}{2} + F(B-2) \\\ = \frac{B-2}{2} + \frac{B-4}{2} + F(B-4) \\\ = \frac{B-2}{2}+ \frac{B-4}{2} + \frac{B-6}{2} + F(B-6) $$

With conditions, $f(1) = f(2) = 0$

$f(B) = \frac{B}{2} + (\frac{B}{2} - 1) + (\frac{B}{2} -2) + \cdots + 1$.

$f(B)$ = Sum of first $\frac{B}{2}$ natural numbers.

Lets call $M = \frac{B}{2}$
$f(B) = \frac {M \times (M-1)}{2}$

You can notice that answer for $2N$ and $ 2N+1$ will be the same.

Solution:

Setter's solution can be found here
Tester's solution can be found here

PROBLEM LINK:

Practice
Contest

Author: Devendra Agarwal
Tester: Anudeep Nekkanti
Editorialist: Amit Pandey

DIFFICULTY:

Simple.

PREREQUISITES:

Dynamic programming or combinatorics.

PROBLEM:

Dehatti wonders how many ways can his team score exactly $R$ runs in $B$ balls with $L$ wickets. Given that each ball can result in $4, 6, 0$ runs or a wicket(wicket won't add anything to score).

QUICK EXPLANATION:

Suppose we want to make $R$ runs in $B$ balls, having $X$ number of $4$'s, $Y$ number of $6$'s, ($W \le L$) number of wickets and $Z$ number of $0$'s. So there will be $4X + 6Y = R$ and $X+Y+W+Z = B$. If $(x,y,z,w)$ is a particular solution to given equations, then number of ways of arrangement will be $\frac {B!}{(x!)(y!)(w!)(z!)}$. We have to add all such cases, and the given time limit is sufficient for it.

EXPLANATION:

First of all, pre-calculate the value of $ ^n C_{r}$ which can be done using a simple dynamic programming approach. You may refer this link for the more details.

As batsman has to make $R$ runs in $B$ balls, if $R > 6B$, there will not be any way of doing it.

Suppose he makes $R$ runs in $B$ balls, with at-max $L$ wickets. So, we will have the following equations.

$4 \times \text{fours} + 6 \times \text{sixes} = R \\ \text{fours} + \text{sixes} + \text{wickets}(\le L) + \text{zeros} = B$

There will be many solutions to the given equations for particular values of $R$,$B$ and $L$. We have to consider each one of them.

Let us consider that a particular solution of the equation is fours = $X$, sixes = $Y$, wickets = $W$ and zeros = $Z$, or $(X,Y,Z,W)$ is a solution to the given equations.

So, number of ways of arranging $X \hspace{2 mm}4's$, $Y \hspace{2 mm}6's$, $W$ wickets ans $Z \hspace{2 mm}0's$ can be calculated easily using the formula.

$\text{Ways} = \frac {B!}{(X!)(Y!)(Z!)(W!)} \\ ={B \choose X} {B-X \choose Y} {B-X-Y \choose W}$

Values can be used from initially calculated ${n \choose r}$ values . Take care of modulus as well.

T only thing remains is to produce all the triplets $(X,Y,Z,W)$.

We can run a loop on number of sixes varying from 0 to min(B,R/6),number of fours will be fixed i.e.

Number of fours = (R -6*sixes)/4 if ((R - 6*sixes) % 4 == 0)

And we can loop over number of wickets from 0 to L.

Number of zeros = B-sixes-fours-wickets

The following piece of self explanatory code will do all the calculations.

for(int six=0; six*6 <= r && six <= b; six++) {
        int other = r - six*6;
        if(other % 4 == 0) {
            int four = other/4;
            for(int wicket=0; wicket <= l; wicket++) {
                if(six + four + wicket <= b) {
                    long long cur = C[b][six];
                    ( cur *= C[b-six][four] ) %= 1000000007;
                    ( cur *= C[b-six-four][wicket] ) %= 1000000007;
                    ways += cur;
                }
            }
            ways %= 1000000007;
        }
    }

Solutions:

Setter's solution can be found here .
Setter's another solution can be found here .
Tester's solution can be found here.

PROBLEM LINK:

Practice
Contest

Author: Devendra Agarwal
Tester: Anudeep Nekkanti
Editorialist: Amit Pandey

DIFFICULTY:

Medium.

PREREQUISITES:

Dynamic programming and Data Structure(stack).

PROBLEM:

You are given a character parenthesis ( having $[,],{,},<,>,(,) $) array and an integer array. You need to find the maximum sum sub-array in the integer array such that the corresponding sub-array in the character array has balanced parenthesis.

QUICK EXPLANATION:

The given problem can be solved using a dynamic programming approach quite similar to maximum subarray problem. We need to take care of balanced parenthesis, which can be done using a classical approach.

EXPLANATION:

First Problem:
How to solve maximum sum sub array problem using Kadane ALgorithm, which is a classical dynamic programming problem.

def max_subarray(A):
    max_ending_here = max_so_far = 0
    for x in A:
        max_ending_here = max(0, max_ending_here + x)
        max_so_far = max(max_so_far, max_ending_here)
    return max_so_far

Second problem:
Given a character parenthesis array, check if it is balanced or not.

1) Declare a character stack $S$.
2) Now traverse the expression string expression.

• If the current character is a starting bracket then push it to stack.
• If the current character is a closing bracket, then pop from stack and if the popped character is the matching starting bracket then fine else parenthesis are not balanced.

3) After complete traversal, if there is some starting bracket left in stack then “not balanced”.

Original Problem:
Now back to original problem. Traverse the character array and if there is a closing brace at position $i$, determine the largest index($j < i$) such that $[j,i]$ is balanced. We can this in one pass of the character array using a stack. The approach is similar to the second problem given above.

for(int i=0;i<=N+1;i++)
hsh[i] = 0;     // This array will store j for each i.
stack<int> st;
st.push(0);
for (int i = 1; i <= n; i++) {
    if (!st.empty()) {
        // check if top of stack is opposite of current parenthesis.
        if (closingBracket(s[i]) && s[st.top()] == opposite(s[i])) {
            hsh[i] = st.top(); // We found j for the i.
            st.pop();
        } else {
            st.push(i);
        }
    } else {
        st.push(i);
    }
}

When we are at index $i$, we may consider what we have solved problem upto index $i-1$, and we have created an array $DP[ \hspace{1 mm}]$. Where, $DP[j]$ stored the maximum sum ending at index $j$.

Dynamic Programming recurrence:

Let us call a sub-array valid, if its corresponding character array is balanced. Let dp[i] denotes maximum sum valid sub-array ending at position $i$. So recurrence for $DP$ will be as follows.

$DP[i] = max$ $(DP[i], dp[hsh[i] - 1] + sum(hsh[i], i))$

$hsh[i] \text{ is the largest j (j < i) such that segment} [j,i] \text{ is the balanced.} $

The given recurrence is using the simple fact if expressions $E_{1}$ and $E_{2}$ are balanced, expression $E_{1}E_{2}$ is balanced.

For finding out overall maximum sum sub-array we can iterate over each $i$ and take maximum of $DP[i]$.

Solutions:

Setter's solution can be found here.
Tester's solution can be found here.

PROBLEM LINK:

Practice
Contest

Author: Devendra Agarwal
Tester: Anudeep Nekkanti
Editorialist: Amit Pandey

DIFFICULTY:

Simple.

PREREQUISITES:

Dynamic programming and basic mathematics.

PROBLEM:

You are given a function f which is defined as: $$f(N) = 1^N 2^{N-1}.....N^1$$ Find $$\frac {f(N)}{f(r)f(N-r)} \mod M$$

QUICK EXPLANATION:

Let $r = \min(r,N-r)$. There will be three cases: $x \le r$, $r < x \le N-r$ and $N-r < x \le N$. Calculate power of $x$ in each of the case and multiply them taking modulo $M$.

EXPLANATION:

The give problem can be solved using simple dynamic programming approach.

Let $r = \min(r,N-r)$ and call $ F(N,r) = \frac {f(N)}{f(r)f(N-r)} $.

Case 1$(x \le r)$:

Power of $x$ in $f(N)$= $N -x+1$.
Power of $x$ in $f(r)$= $r-x+1$.
Power of $x$ in $f(N-r)$= $(N-r)-x+1$.
Hence, Power of $x(\le r)$ in $F(N,r)$= $(N-x+1) - (r-x+1) - ((N-r)-x+1) = x-1$.

Case 2$(r < x \le N-r)$:

Power of $x$ in $f(N)$= $N-x+1$.
Power of $x$ in $f(r)$= $0$. as $(x > r)$
Power of $x$ in $f(N-r)$= $(N-r)-x+1$.
Hence, Power of $x$ in $F(N,r)$= $(N-x+1) - ((N-r)-x+1) = r $.

Case 3$(N-r < x \le N)$:

Power of $x$ in $f(N)$= $N-x+1$.
There will not be any term corresponding to denominator. Hence, Power of $x$ in $F(N,r)$= $(N-x+1)$.

As, there can be large number of queries. We need to do some pre-processing to give results. As, results to first and third case doesn't depend on the value of $r$, we can pre-process them and store.

    //Case I : For the given value of r, fordp[r] will store multiplication
      of all x corresponding to the first case.
    for(int i=1;i<=N/2;i++)
         fordp[i] = (fordp[i-1]*binpow(i,i-1,M))%M;

In case 2, it can be noticed that power of $x$ depends on $r$ and the distance of $r$ and $N-r$ from $N/2$ will be the same. So, we can store multiplication of terms which are equi-distance from center in an array. So, that we can get value of $Midr = \prod_{r+1}^{N-r} x$ in constant time.

     //Case 2 : You can get Midr in O(1) time.
     if(N&1)
          betdp[N/2] = N/2 +1;
     else
          betdp[N/2]=1;
     for(ll i=N/2-1;i>=1;i--)
      betdp[i] = ((ll)((betdp[i+1]*(i+1))%M)*(ll)(N-i))%M;

Case 3 will not depend on the value of $r$, so we can do it similar to case 1.

    //Case III
     for(ll i=1;i<=N/2;i++)
           backdp[i]= (backdp[i-1]*binpow(N-i+1,i,M))%M;

Finally you can calculate the output easily. See Setter's code for the detailed implementation.

Second case i.e. calculating $\prod_{r+1}^{N-r} x % M$ can also be done using the segment tree. In the segment tree, a node will store the multiplication of both of the children mod $M$. Refer this wonderful tutorials for the more details on segment tree. See tester's code for the implementation of this approach.

Solutions:

Setter's solution can be found here.
Tester's solution can be found here.